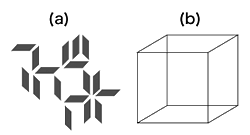
The laboratory for Perceptual Dynamics takes a “complex systems” approach to visual information processing. Visual information is considered as, rather than a static image, a pattern that develops over time. The eyes are continuously moving, giving rise to various kinds of changes in the ongoing stimulation. But even if the eyes do not move and the external information remains essentially unchanged, the pattern we see changes substantially over time. The most striking manifestations of this are perceptual switching in so-called multi-stable and ambiguous figures (Fig. 1). To call these figures multi- or bi-stable is actually misleading; no stability is involved. As these examples show, perceptual functions can hardly be understood in terms of systems going from input (for instance, a given set of features) to a stable state, in which output is produced but no further changes occur with time.
The laboratory is interested in the role of time in perceptual experiences as well as in their underlying neural signals. Two aspects of the neural signal are of particular interest: the problem of how information is encoded in precisely timed spike sequences (Gong & van Leeuwen, 2007) and how neural patterns of synchrony develop over time (Ito et al, 2007). These timing patterns could be described as ever changing. Their motions can be characterized as “wandering.” Wandering dynamics offers an antidote to the notion that visual information processing systems are geared to approaching stable output states.
In our efforts to model the visual system, we try to incorporate such “wandering dynamics” in a principled manner. A principled approach involves finding a theoretical description of the goals of the visual system (what information is being processed, what the outcome should be, and how this aim could be secured in the best possible way), followed by an algorithm to achieve the stated goal in the best possible way, given the known physical constraints of the visual signal.
For solving these kinds of problems, computational theory has played an important role in the history of cognitive science, in particular through the work of David Marr. More recently, its impact has waned under the emergence of rivaling approaches, based on neural networks and dynamical systems theory. These approaches often rely on haphazard, tinkered solutions. For dynamical systems, principled solutions are available within the framework of mathematical control theory. To date, mathematical control theory is predominantly used for analysis and design of various artificial systems in mechanics and engineering. True, its most important results so far - stability, optimality, and invariance theorems in the realm of linear systems- made it widely popular in engineering. But Norbert Wiener, who laid the foundations of mathematical control theory under the heading of Cybernetics, initially meant it as a much broader theory relevant to the organization of biological systems, including the mind. Yet, constructive results in this domain were lacking.
In particular, what have been lacking are results for designing dynamical systems which may possess unstable target dynamics, with nonlinear parameterizations and in the presence of uncertainties. Some of these results were recently discovered in the lab (e.g. Tyukin, Prokhorov, & van Leeuwen, 2007; Tyukin, van Leeuwen, 2006; Tyukin, Tyukina & van Leeuwen, 2007). When applied to the problem of visual pattern recognition, these results show that, contrary to intuition, a system capable of invariant and robust pattern recognition should generally be unstable in the vicinity of its target. In such systems minor mismatches, even in absence of external noise, induce a non-zero probability of switching from one representation to another. Thus, a principled approach to modeling pattern recognition reveals why the real system has the dynamics that it does.
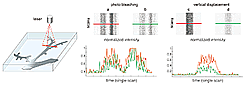
Besides for pattern recognition, the tools developed can be considered useful in a variety of other domains, wherever instability or substantial uncertainty is an issue. This includes nonlinear systems in electronic and automotive applications There are also, however, several interesting applications which more directly involve the brain. One application, in cooperation with the lab led by Alexey Semyanov, involves analyzing fast dynamic changes in the dendrite morphology on the basis of images obtained from two-photon microscopy (Fig. 3).
This project requires tracking of rapid changes in dendrite geometry as well as spine diameter, while at the same time ensuring invariance to distortions due to photo bleaching and tiny physical movements of objects in the slice. The data is a temporal sequence of intensity values along a specified scanning line. The mathematical description of these effects assumes, besides nonlinear parameterization of uncertain variables (e.g. position and concentration of a dye), multiple representations of the same data. Thus application of conventional stability-based techniques, which require linearity and uniqueness, is not an option. Instead, “wandering” dynamics allows finding each of the multiple stimulus representations.
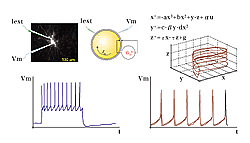
In another project, which also involves scientists from Eindhoven University of Technology, the Netherlands, and Nizhny Novgorod, Russia, we applied our techniques for the sake of monitoring, discovery, identification and modeling of the spiking behavior of neurons in slices (Fig. 4). Here, as we have shown analytically, the deficit of measurement information does not allow employing approaches that guarantee uniform convergence of model parameter estimates. Hence, a “wandering” alternative was provided.
The models for pattern recognition, including the application to two-photon microscopy and the algorithm used for parameter estimation in the Hindmarsh-Rose model neuron are both applications of an approach in adaptive control theory that allows non-stable target behavior. We consider such a theory an essential instrument for progress in theoretical neuroscience.